Arithmetic and Number Properties
Types of Numbers
Any counting number including negative numbers (e.g. -3, -1, 2, 7…but not 2.5)
Real Numbers:
Numbers that appear on the number line (i.e., one that is not imaginary) including pi, the square root of 2, etc.
A positive number is greater than 0, a negative number is less than 0.
Order of Operations: PEMDAS
Complete any arithmetical operation in the following order:1. Parentheses
2. Exponents
3. Multiplication/Division
4. Addition/Subtraction
Example:

You can remember PEMDAS as “Please Excuse My Dear Aunt Sally,” or “Purple Eggplants Make Delicious Afternoon Snacks,” or my personal favorite, “Pandas Explore Many Delightful Asian Scenes”
Commutative, Associative, and Distributive Properties
The Commutative Property:
The Associative Property:
The Distributive Property:
The Commutative and Associate properties do not work with subtraction or division.
Prime Numbers
A prime number is one that is divisible only by itself and 1. In other words, a positive integer with exactly 2 positive divisors. This includes 2, 3, 5, 7, and 11, but not 9, because 9 = 3 x 3.
1 is not a prime. 2 is the smallest prime and the only even prime.
Memorize all primes below 60: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59…
Factorization
If X can be multiplied by Y to get Z, assuming all of these are positive integers, then X and Y are considered factors of Z.
The prime factorization of a number is dividing it into its constituent primes. So for 21, this is 3 x 7; for 60, 2 x 2 x 3 x 5. 7644 = 2 x 2 x 3 x 7 x 7 x 13. To find the prime factorization of 60, you can use 60 = 30 x 2 = 15 x 2 x 2 = 5 x 3 x 2 x 2.
16 has five positive divisors: 1, 2, 4, 8, 16.
40 has 8: 1, 2, 4, 5, 8, 10, 20, 40.
To find how many factors 720 has, first find its prime factorization: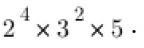 All of its factors will be of the form
All of its factors will be of the form  Now there are five choices for a (a= 0, 1, 2, 3, or 4), three choices for b (b = 0, 1, or 2), and two choices for c (c= 0 or 1). The total number of factors is therefore 5 x 3 x 2 = 30. 720 has 30 factors.
Now there are five choices for a (a= 0, 1, 2, 3, or 4), three choices for b (b = 0, 1, or 2), and two choices for c (c= 0 or 1). The total number of factors is therefore 5 x 3 x 2 = 30. 720 has 30 factors.
The greatest common factor (aka greatest common divisor) of two numbers is the biggest factor shared by two numbers. The GCF of 12 and 30 is 6 – it is the biggest divisor they both share. The easiest way to find the GCF is to take the prime factorization and multiply all of the primes that appear in both numbers. So since 56 = 2 x 2 x 2 x 7 and 70 = 2 x 5 x 7, the GCF is 2 x 7 = 14. If two numbers share no primes, the GCF is 1.
The least common multiple of two numbers is the smallest positive integer with both numbers as a factor. The LCM of 4 and 6 is 12 – it is the smallest number that has both 4 and 6 in its divisors. The LCM of 9 and 15 is 45; the LCM of 7 and 21 is 21, because 21′s factors are 1, 3, 7, and 21. To find the LCM of any two numbers, take the prime factorization of each number, find what prime factors appear in both, and multiply one of each of the shared primes and then by all the unshared primes. So for example, 12 = 2 x 2 x 3, and 56 = 2 x 2 x 2 x 7, so the LCM of 12 and 56 is (2 x 2) [shared primes] x 3 [12's unshared primes] x (2*7) [56's unshared primes] = 168. The largest possible LCM for any two numbers is one multiplied by the other.
Divisibility Rules:
3 : sum of digits divisible by 34 : the last two digits of number are divisible by 4
5 : the last digit is either a 5 or zero
6 : even number and sum of digits is divisible by 3
8 : if the last three digits are divisible by 8
9: sum of digits is divisible by 9
Fast Fractions
Absolute Values
The absolute value of a number is its distance from a number line.
|x| = x, |-x| = x
Percentages
“Percent” = per 100;

To find what percent some part is of a whole, use
To find what percent some part is of a whole, use
For example, if 120 of 800 people in a town smoke, then
of the townspeople smoke. Most percentage problems break down into identifying the part, the percent, and the whole, one of which will be unknown.
If p percent of x is y, then
Percent change : % change = change/original value
If the price of something goes from $40 to $52, the percent change
This can also be written as (change x 100) / original value. So here,
If something increases by 20%, then decreases by 5%, it is not the same as if it increased by 15%. For example: 100 -> 120 -> 114, whereas if 100 increased by 15% it would be 115.
If a price falls by 15%, you can multiply the original value by (1 – 0.15 = 0.85) to find the new value. 250% of the original price is the same as 150% more than the original price, and to find either you’d multiply the original price by 2.5.
Ratios
Ratios let us compare the proportions of two quantities. If there is a 2:5 ratio of boys to girls at a school, that means that for every 5 girls, there are 2 boys. So there could be 2 boys and 5 girls, 20 boys and 50 girls, 200 boys and 500 girls, etc.
Ratios are given by x:y, x to y, or x/y. If a question says “for every x there is/are a y,” you are most likely dealing with a ratio question. Ratios can also be x:y:z.
Ratios can be simplified like fractions. 3:6 is the same as 1:2.
Remember that if there is a 2:5 ratio of boys to girls at a school, the ratio of boys to total students is 2:(5 + 2) = 2:7. 2/7 of the students are boys.



















